Jacob Gaboury

PhD Candidate, Media, Culture, and Communication, NYU

In her 2004 book Network Culture Tiziana Terranova suggests that in information theory, communication is concerned primarily with the problem of signal and noise, and that information flow has come to displace the question of linguistic representation and cultural identity from the center of cultural struggle. [1] That is, those sites which have most concerned queer theory for the past 30 years – identity, interiority, performance, representation, affect – are at best vacated by new media technologies and at worst appropriated in the implementation of new forms of soft control, which Alexander Galloway has famously termed ‘protocol.’ [2] Under this schema, we each become equally legible in our difference, the specificity of which becomes insignificant. We are compelled in fact to identify and define ourselves within a given set of legible identity parameters – race, gender, sexuality, age, taste, preference, etc. While individual complexity and diversity no doubt exist, the technologies that structure our communication function in a state of willful indifference to such distinctions. In effect, the self is black-boxed, reducing it to limited set of legible input and output signals.

This is not to say that identity politics loses its meaning and function in the network society. Indeed new media technologies thrive on the differentiation offered by such categories. Rather, I would suggest that such differences no longer function clearly as sites of resistance to power, as they have become incorporated into the logic of the control society. Identity has become technological, it has become mobilized in the service of a complex socio-political structure that is the outgrowth of information and network technologies. This is not to suggest that identity politics be abandoned, nor would I suggest that the capacity to set aside identity politics in such a way is an evenly distributed privilege. [3] As numerous authors have shown, identity categories continue to be sites in which power is produced and resisted through new media technologies. [4] Yet it would be naïve to ignore the ways in which identity as a category has been itself transformed by computational technologies. Indeed I would suggest that a functional contemporary critique must be invested in the material and historical specificity of the technical objects that produce it, and not simply their cultural expression in the particularities of identity and difference.

Yet we need not abandon queer critique altogether. In fact, I would argue that queerness is the ideal lens through which we might mobilize a politics that engages and critiques computational technology, one that exists within an exceptional space produced by but outside its dominating structures. Here queerness is not an object but rather a methodology, founded in the long history of queer engagements with the anti-social, the negative, and the outside. This theoretical history arguably first gains prominence in the work of Leo Bersani, who in his 1987 essay “Is The Rectum A Grave?” seeks to resist the desire to make sex the basis for a rational political position, identifying what he sees as a tyranny of selfhood in the attempt to delimit that which is acceptably political through the body and through sex. [5] To quote Jack Halberstam’s reading of Bersani: “we clean sex up […] by making it about self-fashioning instead of self-shattering.” [6] Written in an era in which homosexuality was quite literally associated with self-destruction and death through HIV infection, Bersani does not refuse or apologize for such acts, suggesting instead that “if the rectum is the grave in which the masculine ideal of proud subjectivity is buried, then it should be celebrated for its very potential for death.” [7] Lee Edelman takes this one step further, arguing in No Future (2004) that the queer subject has always been bound epistemologically to negativity, to nonsense, to antiproduction, and to unintelligibility. [8] Rather than fighting this characterization and attempting to make queerness productively legible, Edelman suggests we embrace this negativity and refuse participation in the sacrifice of our queer present for the promise of some utopian future. [9]

Applying this gesture to technology, we might posit a queer technics in the exploration of the failure of technical objects and systems, of that which is viewed as improper or anomalous but which nonetheless comprises our everyday experience of technology. If we imagine communication to be structured by technical systems, as Terranova has suggested, then implicit in such a structure there exists an alternative to connection, transmission, and identification through their negation in signal failure, and illegibility. It is here that we might identify a queer computing – outside the imperative of successful communication. It is those forms of computation that fail, break down, recur, and run forever, and models of computing that are outside of or beyond so-called ‘universal’ Turing computation – that is, those processes which disappear or recede from computational forms of knowing. [10] This is not simply a speculative re-reading of technical objects, or a ‘queering’ of existing practice, but an attempt to identify a queerness within the technical object itself, a concern that reaches back to the early 20th century foundational crisis of mathematics, and indeed to the origins of the theory of computing. To explore the possibility of a queerness beyond these limits, I will turn to an anecdote from two foundational queer figures in the early history of computing, and an encounter that took place in 1939 at Cambridge University. While it may seem strange to return to this early moment the history of computation in order to posit a contemporary queer politics, doing so allows us to argue that such queerness exists within the theory of computation from the very beginning. Moreover, by situating this work historically, we can address computation in those primitive moments of experimentation and emergence before the field crystallizes into a discipline and an ideology. In doing so we discover a kind of liminal technical space of something not yet actualized.

In the spring of 1939, Ludwig Wittgenstein taught a course at the University of Cambridge on the foundations of mathematics, a topic that occupied much of his work from 1922 through to the end of the Second World War. That same year another young scholar and philosopher began research at the university. After two years working under Alonso Church at the Institute for Advanced Study in Princeton, New Jersey, Alan Turing took up a position as an untenured research fellow at Cambridge, having failed to acquire a full lectureship. Turing and Wittgenstein had been introduced at a party the summer of 1937, but it was not two years later that they would have any meaningful interaction. That spring, Turing was also teaching a course on the foundations of mathematics that shared the same name as Wittgenstein’s lecture. Perhaps intrigued, Turing enrolled, and over the course of the semester, Turing engaged in a lengthy dialogue with Wittgenstein, challenging and outright refusing much of his thoughts on logic and mathematics. [11] Despite their disagreement, I see this as a pivotal moment in the history of computing, in which two queer figures engage with the limits of mathematical knowledge and computability. [12]

As a young man, Wittgenstein had thought logic could provide a solid foundation for a philosophy of mathematics. Now in his fifties, he denied outright there were any mathematical facts to be discovered. For Wittgenstein, a proof in mathematics does not establish the truth of a conclusion, but rather fixes the meaning of certain signs. For him the “inexorability” of mathematics does not consist in certain knowledge of mathematical truths, but in the fact that mathematical propositions are grammatical, a kind of language game through which meaning becomes fixed. In one particularly memorable exchange, Wittgenstein puts forth one of his favorite contradictions – known as Epimenides’ paradox, or the liar’s paradox:

WITTGENSTEIN: If a man says ‘I am lying’ we say that it follows that he is not lying, from which it follows that he is lying and so on. Well, so what? You can go on like that until you are black in the face. Why not? It doesn’t matter […] it is just a useless language-game, and why should anyone be excited?

TURING: What puzzles one is that one usually uses a contradiction as a criterion for
having done something wrong. But in this case one cannot find anything done wrong. 

WITTGENSTEIN: Yes – and more: nothing has been done wrong, […] where will the harm come? 

TURING: The real harm will not come in unless there is an application, in which a bridge may fall down or something of that sort. 

WITTGENSTEIN: The question is: Why are people afraid of contradictions? It is easy to understand why they should be afraid of contradictions, etc., outside mathematics. The question is: Why should they be afraid of contradictions inside mathematics? Turing says, ‘Because something may go wrong with the application.’ But nothing need go wrong. [13]
Here Wittgenstein suggests that there exist contradictions, but those contradictions cannot be made meaningful to mathematics, and exist outside of or despite functional applications. Turing responds by coming to the defense of a surprisingly conservative mathematical determinism, arguing that surely mathematics must tell us something of the world, as it allows us to build bridges that don’t fall down and to calculate with great precision measurable truths in the world. Turing accuses Wittgenstein of introducing philosophy into mathematics, that his propositions are not properly mathematical, while Wittgenstein insists that there is nothing philosophical about his conjectures, going so far as to suggest that, in fact, Turing is in full agreement with him despite these protestations. [14]

These debates dominate much of the semester, and it seems Wittgenstein saw it as a challenge to convince Turing of his philosophical position, going so far as to refuse to lecture if Turing was not in attendance. By the end of the semester the two were unable to agree, as though each man were speaking past the other in a language whose words were familiar but, perhaps appropriately, whose meaning seemed to differ. Yet strangely, despite this failure, Turing’s own work and research during the three years prior to the lectures touches on many of the same themes as Wittgenstein’s, addressing those invisible or unknowable truths that escape mathematical calculation through computation. While Wittgenstein seeks to discount the importance of contradiction to the study of mathematics, much of Turing’s work on the foundations of computation is explicitly interested in these contradictions, and in identifying them as externalities to a functional system of calculation. While the two are clearly are at odds over the significance of these exceptions, both are nonetheless explicitly preoccupied with these queer externalities.

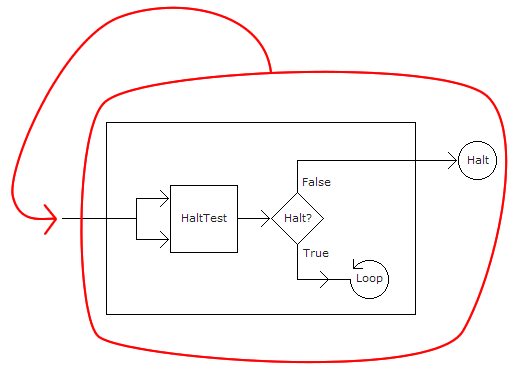
Turing’s most famous work on this subject is On Computable Numbers, published in 1936, in which he establishes the definition of computable numbers as “the real numbers whose expressions as a decimal are calculable by finite means,” stating that “a number is computable if its decimal can be written down by a machine.” [15] Turing expands his thesis, proving that his formalism was sufficiently general to encompass anything that a human being could do when carrying out a definite method. Importantly, Turing also established in this work the limits of computation, identifying the existence of uncomputable problems that cannot be solved through a definite method. [16] The most famous such problem is the halting problem, in which an algorithm is built to calculate whether a given program will halt and produce a solution, or run forever. If such a program were to exist, we might in turn apply it back onto itself, asking it to find if it will ever halt, and in doing so creating a paradox not dissimilar to the case of the liar.

More interesting to this project, however, is a supplementary paper published in 1939, titled Systems of Logic Based on Ordinals, in which Turing asks if it is possible to formalize those actions of the mind that do not follow a definite method – mental actions we might call creative or original in nature. There exist certain sets of uncomputable problems which are functionally solvable by human means, but for which there is no definite method for calculating an answer. Here Turing suggests the impossibility of accounting for this intuitive action through computation, stating:
Mathematical reasoning may be regarded rather schematically as the combination of two faculties, which we may call intuition and ingenuity. The activity of the intuition consists in making spontaneous judgments, which are not the result of conscious trains of reasoning. [17]

It is unclear how such intuition functions, or how to understand and successfully implement it, but Turing’s biographer Andrew Hodges suggests that “at this time [Turing] was open to the idea that in moments of ‘intuition’ the mind appears to do something outside the scope of the Turing machine.” [18] That is, outside of computation as Turing has defined it. [19]

But what does this computational form look like? What are the objects of queer computing? While universal Turing computation is considered by many to be the inspiration for the stored program computer architecture developed by John von Neumann in 1946, along with subsequent developments that make possible the majority of contemporary computational technologies, there nonetheless exists a field of computer science devoted to the study of computing beyond the limits set by Turing in 1936, a field concerned with what is called hypercomputation or super-Turing machines. Returning to that most famous externality to Turing computation, the halting problem, we see a clear exception to the procedural definition of computation in the form of infinite recursion, or the need to complete an infinite number of steps in a finite amount of time.

In hypercomputing the machine imagined to perform such a task is called a Zeno Machine, named after the pre-Socratic Greek philosopher Zeno of Elea, famous for his paradoxes of motion. [21] In Zeno’s dichotomy paradox, he conjectures that in order for an object to move through space to a goal it must first move halfway there, and in order to move halfway it must move a quarter of the way, and eighth, a sixteenth, and so on. If in this way we can divide space into an infinite number of increments, then motion is impossible, as it requires us to make an infinite number of steps in a finite period of time. Yet despite this, objects appear to move in space and arrive at goals, defying logic despite the laws by which we understand the world to function. Applying Zeno’s paradox to the material world we might try and divide space itself into smaller and smaller pieces, yet no matter how small we divide it there must nonetheless always be something that separates those pieces from one another, an unquantifiable “nothing” that exists beyond or outside materiality itself. Failing this no such division is possible and all must be understood as part of a larger singularity, a univocity of difference that is nonetheless one. A Zeno Machine, then, is one that is capable of performing an infinite number of procedural computations in a finite period of time, of collapsing the paradoxical into a single comprehensible unit, a gesture Turing referred to suggestively as “calling the oracle.” [20]

I would suggest that these speculative technologies might function as a critique of binary or digital systems, which function by dividing the world into quantifiable pieces. Zeno’s paradox of motion is therefore also the paradox of computation, that things exist beyond our delimitation of the world into phenomenologically knowable objects, and that while mathematics and by extension computation function despite these contradictions there nonetheless exists a Beyond that is illegible, or that we fail to recognize. In seeking alternatives to ways of knowing that are mediated by computing technology, it is my hope that we might identify an alternate logic of illegibility that might be opened up to produce a critique of new media objects. In choosing this, perhaps the earliest moment at which such an inquiry is made possible, it seems meaningful that such questions are being posed by two queer men who met only briefly and, perhaps appropriately, were unable to come to an agreement, or even understand the questions the other sought to answer. While it is no doubt true that queerness is not the only means by which we might ask these questions of technology, or through which we might seek an alternative to the universalizing structures of new media technologies, it is my suggestion that queerness is the ideal lens through which to examine a negativity that exists outside of or beyond – one that begins with two queer men in the earliest moments in the history of computation.

References:

1. Tiziana Terranova, Network Culture: Politics for the Information Age (London: Pluto Press, 2004), 10.
2. Alexander Galloway, Protocol: How Control Exists after Decentralization (Cambridge: MIT Press, 2004).
3. A politics of negation, refusal, and dismissal has been taken up by numerous scholars in recent years, including Agamben (1993), Tiqqun (2001), and Galloway and Thacker (2007). I would argue that a queer politics of negation predates these by several decades, going back at least to Guy Hocquenghem’s Homosexual Desire (1972), but particularly problematic in each of these formations is the assumption that the refusal of identification is equally possible for all subjects. Many forms of difference, such as racial difference, are often imposed from without, and cannot be made invisible to power.
4. See, for example, Lisa Nakamura and Peter Chow-White, eds., Race After the Internet (New York: Routledge, 2011).
5. Leo Bersani, “Is the Rectum a Grave?,” October 43, Winter (1987): 197-222.
6. Judith Halberstam, The Queer Art of Failure (Durham: Duke University Press, 2011), 149.
7. Bersani, “Is the Rectum a Grave?,” 29.
8. Lee Edelman, No Future: Queer Theory and the Death Drive, (Durham: Duke University Press, 2004).
9. I acknowledge the problematic pairing of Edelman and Halberstam’s work here, and I don’t mean to suggest that the two are in agreement over the nature of failure and negativity in a queer politics. In part, I mean for this critique to be an expansion of Edelman and Bersani’s work beyond the deeply psychoanalytic and literary frame of their work. In applying failure to a technical object using a materialist critique, my hope is to introduce a politics to their theory, which is often criticized by Halberstam and others as lacking a clear political investment.
10. It is important to note that I do not include “noise” or “glitch” in this list of queer failings. Noise is excluded in part because it is an important and existing part of any information system. As Michel Serres famously described in The Parasite (1980), noise serves as the “third man” in all communication and is by no means external to or outside. Furthremore, as Jussi Parikka has noted in his Digital Contagions: A Media Archaeology of Computer Viruses (2007), far from anomalous these minor failings are in fact highly productive to third wave cybernetics and contemporary capitalism. As such this queer critique cannot be applied universally or unquestioningly to all technical failings.
11. These encounters have been collected and recorded based on the notes of four students who attended the lecture, and were subsequently edited and published. As such they form an imperfect, but essential archive.
12. While I choose to read Wittgenstein as a queer figure here, I acknowledge the controversy surrounding this analysis for many philosophers and historians. While Wittgenstein’s homosexuality has at this point been widely acknowledged, until the 1980s it was a subject rarely discussed among colleagues or in the many biographies written about his life and work. Yet despite concerns over the veracity of claims to the physical nature of Wittgenstein’s sexuality, I see him as an ideal queer figure for the purposes of this critique due precisely to this difficulty in reading him as a legibly sexual. That is, due to the ways in which his queerness becomes illegible when read anachronistically from the present.
13. Cora Diamond, ed. Wittgenstein’s Lectures on the Foundations of Mathematics: Cambridge, 1939 (Ithaca, NY: Cornell University Press, 1976) 416.
14. Cora Diamond, ed. Wittgenstein’s Lectures on the Foundations of Mathematics: Cambridge, 1939, 67.
15. Alan Turing, “On Computable Numbers, with an Application to the Entscheidungsproblem” Proceedings of the London Mathematical Society, Series 2, 42 (1937): 230.
16. Turing’s work on uncomputability does not emerge from nowhere. It is informed by several decades of debate in the early history of mathematics – what is often referred to as the foundational crisis of mathematics, or Grundlagenkrise der Mathematik – over the question of whether mathematics had any foundation that could be stated within mathematics itself without suffering from irresolvable paradoxes. This led to competing schools of thought, the most important of which was Hilbert’s program, named after the German mathematician David Hilbert. The program proposed to ground all existing theories to a finite, complete set of axioms, and provide a proof that these axioms were consistent. However, in 1931 Kurt Gödel’s incompleteness theorems showed that any consistent system with a computable set of axioms which is capable of expressing arithmetic can never be complete, that it is possible to prove a statement to be true that cannot be derived from the formal rules of the system. Turing would take Gödel’s work further, applying this theorem to the concept of computability, defined as that which can be stated within a formal system and may therefore be executed by a machine with a procedural grasp of computational logic.
17. Alan Turing, “Systems of Logic Based on Ordinals” Proceedings of the London Mathematical Society, Series 2, 45 (1939):
18. “Alan Turing: one of The Great Philosophers” on Andrew Hodges’ official website, accessed April 1, 2013, http://www.turing.org.uk/philosophy/ex4.html
19. This train of thought belongs to a field in the philosophy of mathematics known as “intuitionism.”
20. In computability theory, such a theoretical machine is called an ‘oracle machine,’ and can be understood as a Turing machine connected to a black box called an ‘oracle.’ The oracle is capable of solving some problem that is otherwise unsolvable. It is not assumed to be a Turing machine or a computer program, it is explicitly unknowable, a black box whose only significance is in its functional output.
21. Zeno might in many ways be regarded as the prototypical queer technologist. Like many Greek men, he participated in homosexual erastes-eromenos mentor relationships, and was loved and mentored by Parmenides of Elea, the founder of the Eleatic school of philosophy which maintained that the true explanation of things lies in the conception of a universal unity of being, a concept taken up by Scotus, Heidegger, and Deleuze, among others.

Bio:

Jacob Gaboury is a PhD candidate in the department of Media, Culture, and Communication at NYU and a staff writer for the art and technology organization Rhizome at the New Museum of Contemporary Art in New York City. His work is concerned with media history, art and technology and queer theory. His dissertation is titled Image Objects: Computer Graphics at the University of Utah, 1965-1979, and it deals with the early history of 3D object simulation and the shift toward object oriented paradigms in computer science beginning in the late 1960s. He is the 2013-2014 IEEE Life Members Fellow in Electrical History, a 2013 Lemelson Fellow of the Smithsonian’s National Museum of American History, and the 2012-2013 ACM Fellow in the History of Computing.
http://www.jacobgaboury.com